МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ДИНАМИКИ ВОЗМУЩЕННОГО ДВИЖЕНИЯ САМОЛЕТА

/

В дальнейшем при исследовании возмущенного движения самолета придется рассматривать системы однородных и неоднородных линейных дифферен­циальных уравнений с постоянными коэффициентами.

Система линейных однородных дифференциальных уравнений, правые части — которых равны нулю, описывают собственное возмущенное движение самолета. Такое движение можно получить, если находящемуся в равновесии самолету сообщить некоторые начальные возмущения, а затем предоставить самому себе.

Если в полете самолет будет подвергаться постоянно действующим возмуще­ниям, то его возмущенное движение будет описываться системой неоднородных урав­нений, правые части которых представляют собой некоторые известные функции времени. Такими функциями могут быть внешние силы, вызванные управляющими воздействиями или какими-либо другими возмущениями, например ветровыми.

Известно, что общее решение системы линейных неоднородных дифференциаль­ных уравнений состоит из общего решения соответствующей системы однородных уравнений и частного решения полной (неоднородной) системы. Общему решению однородной системы соответствует собственное возмущенное движение самолета, а частному — вынужденное. Следовательно, система неоднородных линейных диф­ференциальных уравнений описывает движение, которое можно представить как сумму собственного и вынужденного движений.

При исследовании собственного возмущенного движения самолета выясняется устойчивость опорного движения. Анализ вынужденного движения позволяет опре­делить реакцию самолета на управляющие воздействия и сделать оценку его управ­ляемости.

Для линейных систем обыкновенных дифференциальных уравнений с постоян­ными коэффициентами имеются методы решения, которые приводятся в курсах высшей математики. К ним относится так называемый «классический метод» и метод, основанный на операционном исчислении.

Решение линейных дифференциальных уравнений с постоянными коэффициентами классическим методом

В качестве примера возьмем линейную однородную систему дифференциальных уравнений с постоянными коэффициентами четвертого порядка, записанную в форме Коши. Такие системы в дальнейшем будут встречаться при исследовании устой­чивости иевозмущенного движения самолета.

Пусть имеем однородную систему линейных дифференциальных уравнений (15.7), в которой, s = 1, 2, 3, 4

ааі Ауі — ааі Дyt — ak8 Дуз — Ду« — 0,

где ДУі — отклонения (вариации) параметров движения; a«K — известные постоян­ные коэффициенты.’

Общее решение системы получается из суммы произведений частных решений на произвольные постоянные. Гюэтому вначале надо найти линейно независимые частные решения системы (15.11).

Ищем частные решения в виде

Ays = Aytu (S -1,2,3, 4). (15.12)

Требуется определить постоянные At и Я так, чтобы функции Ал&* удовлетво­ряли системе уравнений (15.11). —

Подставляя (15.12) в (15.11) и сокращая на множитель ew, получим систему линейных однородных алгебраических уравнений относительно Ait As, Аъ и

(ап — Я) Aj + а1гАг + algj4g + a14.i4t *= 0; aiiAl — f (a88— Я) A-t + аиЛ8 +

+ OfejAj = 0; азіАі + Oggi4g -f — (ajj — Я) Аз + О34Д4 == (15.13)

ОцАі + аігАй + аюА» + (a«« — Я) Л4 = 0.

Из курса математики известно, что для получения ненулевых решений таких уравнений определитель системы (15.13) должен быть равен нулю.

Составим определитель системы (15.13) и приравняем его нулю

Раскрывая определитель (15.14), получим уравнение четвертого порядка для определения Я, которое называется характеристическим уравнением для системы (15.11)

Я4 4- с3Я3 + с2Я2 -(- СхЯ -(- а0 = 0, (15.15)

где а0, с(, с2 и а, — коэффициенты характеристического уравнения, которые вы­ражаются через известные постоянные коэффициенты уравнений (15.11).

При решении характеристического уравнения возможны случаи, когда все корни — различные (простые) или все (или часть) корней будут кратными.

Допустим, что все четыре корня уравиеиия (15.15) действительные и различные. Для каждого корня Яд (Л = 1, 2, 3,4) напишем систему уравнений (15.13). Таких систем буДет четыре, из которых определим 16 коэффициентов Ath, A2h, Atk и Atk — Причем в каждой системе уравнений один из коэффициентов будет-произвольным, который можно принять равным единице (например, Аль = 1).

Подставляя найденные значения Я* и Aak в (15.12), получим частные решения системы (15.11)

A«/sfc = Ashe’h*‘ (15.16)

Следовательно, общее решение рассматриваемой системы (15.11) будет иметь вид

Ауі — ClAr1it^lt -(■ С2Ах2£*2* -(- С)Иі8е^5* 4- С^Аце?’**

&Уг — C1Ailet’,t + С2Ам^‘* + СаАаг^г* + С^АцЄ^*1′,

. . , . , , . (ІО.17)

— ^i^8ie 1 + Cai48ae 1 + Са^88е а + £4^34® 4 »

Дyt = CieM + C2tut + CgeM 4- Сі? к**,

где Cit Cs, Cf и С, — произвольные постоинные, подлежащие определению из начальных условий.

Подставлия в (15.17) начальные условия (А«/, = &у№ при t = 0), получим С%Ах + С2АХ14- С8і418 + CtAu = Ауы;

СіАц "Ь С|Лц4 4 С±Ац — Ду2оі (15.18)

СхАц 4* CtAai 4- CgAgg 4* С4ЛМ = Дум;

Сі 4* С* 4" С* 4* Ct = Дг/4о*

Эта система алгебраических уравнений является неоднородной, в ией неизвестными являются произвольные постоянные Ch(k— 1 4), которые можно иайтипо фор­

мулам Крамера Сд = £>д/£>, где D — определитель системы (15.18), составленный из коэффициентов* Aak Dk — определитель, получающийся нз D заменой столбца при ьеишзестиом Ck, столбцом, составленным из свободных членов Дуп.

Из общего решения (15.. 17) видно, что когда все Яд действительные, то откло­нения Ау, изменяются с течением времени по апериодическому. закону н будут воз­растать или убывать в зависимости от знаков корней характеристического уравне­ния Яд. Если все Яд будут отрицательными, то при t-*- оо все &ув -*-0, и, следо­вательно, иевозмущенное движение будет асимптотически устойчивым, так ках все параметры в возмущенном движении будут стремиться к параметрам иевозмуіцен — ного. Если среди корней Яд найдется хотя бы одни положительный, то при t -+• оо все Ду8 будут неограниченно возрастать, и, следовательно, иевозмущенное движе­ние будет неустойчивым. 1

Рассмотрим случай, когда среди простых корней характеристического уравие* ння имеются комплексные сопряженные.

Пусть два корня окажутся комплексно сопряженными, например Ях&=х4- + /V, Яа = к — iv. Этим корням будет соответствовать частное решение

Nig (і, 2) ~ "Ь (s=l> 2, 3, 4),

где постоянные А81 и As2 определяются из решения системы (15.13) и являются комплексными сопряженными числами

Asi = as — ibs и As2 = cs + ibs, тогда

(і, 2) = (as — ib8) е(и+іу) * + (a8 + ibs) e(K lv) * = -= aseyt (tlvt + e~tvt) — “Kt <-lvt —

2 cos vt, t‘vt — e ivt = 2t sin v*,

Пользуясь формулами Эйлера eiv* + e lvt

получим

Ays (1,2) = 2а8еи< cos v< + 26sex< sin vt = Л8еи< sin (vf + ф8)

где і48 = 2 — у/ а + і®, ф8 = arctg ————— новые произвольные постоянные. •

Из (15.19) видно, что частное движение, соответствующее паре комплексных сопряженных корней, будет колебательным с амплитудой Л8еи<, круговой частотой v и фазой ф8. Амплитуда колебаний будет неограниченно возрастать, если веществен­ная часть комплексного корня — положительная (и > 0) и затухать, если и < 0.

В рассматриваемом случае собственное возмущенное движение, описываемое уравнениями (15.11), представляет собой наложение одного колебательного и двух апериодических движений, соответствующих действительным корням ка и Л4.

Обобщая полученные результаты, можно сделать вывод, что для устойчивости невозмущенного установившегося движения необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

Этот вывод получен на основании анализа линейных дифференциальных урав­нений (уравнений первого приближения). Допустимость суждения об устойчивости и неустойчивости невозмущеииого движения по уравнениям первого приближения не является очевидной, потому что нелинейная система заменяется линейной, т. е. одна задача подменяется другой. Может оказаться, что иевозмущениое движение в силу линейных уравнений будет устойчивым, а на самом деле неустойчивым.

Отсюда возникает вопрос, когда уравнения первого приближения полностью решают задачу об устойчивости и неустойчивости невозмущеииого движения. Эту важную задачу механики впервые поставил и решил А. М. Ляпунов.

Приведем без доказательства теоремы Ляпунова; позволяющие судить об устой­чивости и неустойчивости установившихся невозмущениых движений по уравне­ниям — первого приближения.

Первая теорема — Если вещественные части всех корней характеристического уравнения системы первого приближения отрицательны, то иевозмущениое Движе­ние асимптотически устойчиво независимо от членов выше первого порядка малости в дифференциальных уравнениях возмущенного движения.

Вторая теорема. Если среди корней характеристического уравнения системы первого приближения имеется хотя бы одни с положительной вещественной частью, то иевозмущениое движение неустойчиво, независимо от членов выше первого порядка малости в дифференциальных уравнениях возмущенного движения.

Возможны случаи, когда среди кориш характеристического уравнения имеются такие, вещественная часть которых равна нулю, а остальные корни имеют отри­цательную вещественную часть. Во всех этих критических случаях устойчивость (неустойчивость) невозмущеииого движения определяется членами выше -первого порядка малости. При этом задача будет тем сложнее, чем больше число критиче­ских случаев. Ряд задач был решен Ляпуновым и другими учеными.

Непосредственное исследование устойчивости невозмущеииого движения по корням характеристического уравнения является простым лишь для уравнений первого и второго порядка. Для характеристических уравнений третьего и четвер­того порядков получаются сложные и часто непригодные для практического исполь­зования формулы для определения корней. Для уравнений более высоких порядков (л > 4) задача определения корней в виде аналитических выражений неразрешима; корни могут быть определены лишь численно.

Однако для решения вопроса об устойчивости или неустойчивости иевозмущен — ного движения можно не определять корни характеристического уравнения, а надо лишь определить знак вещественной части всех корней.

Косвенные признаки, по которым можно судить о знаке вещественной части корней характеристического уравнения линейных систем с постоянными коэффи­циентами, минуя вычисление самих корней, называются критериями устойчивости.

По критериям устойчивости можно судить об устойчивости линейной системы, определять границы устойчивости и выбирать параметры устойчивой системы.

Критерии устойчивости подразделяются на алгебраические и частотные.

Алгебраические критерии позволяют судить об устойчивости и неустойчивости систем по коэффициентам характеристического уравнения. Имеются различные формы критериев. Наибольшее применение получили критерии Гурвица и Рауса.

Приведем без доказательства теорему Гурвица.

Пусть характеристическое уравнение n-й степени имеет вид

Gn. Xn -J — Сц-i^n -[-••• -[- QjK — j — Uq = 0, (15.20)

в котором все коэффициенты ak — вещественные числа, а On > 0. Построим из ■ коэффициентов с* матрицу Гурвица из п строк и п столбцов: Ai Cft_ 1 ап 0 0 . 0 Аг С/г. з С/г-2 Оп-1 сп . 0 Аз С/г-6 Сп-4 Сп-3 С/г-2 . 0 а4 ап-7 С/г-в С/г-6 С/г_4 . 0 . . . 0 Ап 0 0 0 0 «0

По главной диагонали матрицы выписываются все коэффициенты характери­стического уравнения с последовательно убывающими Индексами, начиная с an_L. Все строки справа от коэффициентов, стоящих иа главной диагонали, заполняются коэффициентами с возрастающими индексами, а слева — с убывающими индексами. На место коэффициентов, индексы которых меньше нуля или больше п, ставятся нули.

Теорема Гурвица. Для того чтобы все корни алгебраического уравнения (15.20) имели отрицательные вещественные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы (15.21) были положительны:

Лі = fln-i > О, А, = I вп-1 °п I > 0………………………….. Д„ = а„Д„_і > 0. (15.22)

I Оп-8 On-* I

В частности, если для уравнения четвертой степени

К* “Ь flgX8 -|- а8Я.* -‘г Со — 0 (а^ =1) (15.23)

выполняются неравенства

а»	I > 0; А8 =	с*	1	0
«і	с»	Ся
Ol	а» 1 *	0	Со	Сі

Лі = с8>0; А* =

>0; Д« = соДя > 0,

то вещественные части всех корней (15.23) будут отрицательными.

Равносильными для уравнения 4-й степени являются условия Рауса—Гурвица, которые имеют вид

a0>0, fl!>0, Og >0, а8>0, R = а^а* — aj — > 0. (15.24)

Из теоремы Гурвица и первой теоремы Ляпунова об устойчивости по первому приближению можно сформулировать критерий устойчивости: если при On > 0 все миноры Гурвица А]., …. Дп положительные, то иевозмущеииое движение асимп­тотически устойчиво независимо от членов выше первого порядка малости.

Найдей границы устойчивости. На границе устойчивости будут равны нулю действительный корень (Я = 0) или вещественная часть комплексных сопряженных корней (Я = IV). Если в характеристическое уравнение (15.20) подставить Я = 0, то получим границу апериодической устойчивости: о0 = 0 или Дп — 0 (при всех остальных положительных минорах Гурвица). Подставляя в уравнение (15.20) вместо Я его значение Я =iv, получим границу колебательной устойчивости: Л„_ t = = 0, причем все остальные миноры Гурвица положительны. Третья граница устой­чивости соответствует бесконечному корню Я = оо, и согласно уравнению (15.20) будет при ап — 0 *.

Между границами устойчивости будет находиться область устойчивости.

Критерий Гурвица предпочтителен для систем порядка п ^ 4, так как позво­ляет в общем виде установить соотношения между физическими параметрами си­стемы, при которых обеспечивается устойчивость.

Для систем порядка п > 5 критерии Гурвица и Рауса сильно усложняются и требуют большого объема вычислительных работ. Если возмущенное движение самолета описывается системой линейных неоднородных дифференциальных урав­нений с постоянными коэффициентами, то общее решение такой системы состоит из общего решения однородной и частного решения неоднородной системы.

Общее решение однородной системы рассмотрено ранее. Частное решение не­однородной системы зависит от вида правой части этой системы. Для нахождении частного решения может быть применен метод вариаций произвольных постоянных, а в случае специальных правых частей метод неопределенных коэффициентов. Эл* методы изложены в курсах высшей математики.

Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом

Наряду с классическим методом в инженерной практике получил распростране­ние операторный метод. Особенно широко, этот метод применяется в теории автома­тического управления полетом летательных аппаратов.

Сущность этого метода состоит в том, что посредством интегрального преобра­зования от систем линейных дифференциальных уравнений переходят к вспомога­тельной системе алгебраических уравнений. Затем находят решение вспомогатель­ной системы, а из него при помощи обратного преобразования получают решение заданной системы дифференциальных уравнений.

В качестве интегрального преобразования обычно используют преобразование Лапласа

Y (р) = Цу (<)]=[30] j t-p*y(t)dt.

о

где параметр р — некоторое комплексное число; у (<) — кусочно-непрерывная и ограниченная функция независимой переменной t, называемая оригиналом; У (р)— изображение функции у (/).

Помимо прямого преобразования существует обратное преобразование Лап­ласа, позволяющее по изображению Y (р) находить оригинал у (г). Сокращенное обозначение обратного преобразования U1 [Y (р)] = у (і).

В курсах операционного исчисления приводятся таблицы прямого н обратного преобразования Лапласа основных функций.

Если оригинал у і), имеющий изображение Y (р), подвергается математической операции (сложению, дифференцированию н т. п.), то для нового оригинала можно найти изображение по формулам, приведенным в табл. 15.1.

В приведенных для дифференцирования формулах величины у0, у0…………. у$~х

представляют собой значения функции у (О и ее производных в начальный момент времени (начальные условия).

При анализе возмущенного движения самолета иногда возникает необходимость определить предельные значения решения дифференциального уравнения по виду

этого уравнения, ие решая его. Например, надо оценить поведение функции у (І) •

Математичес кая операция	Оригинал	Изображение
Исходное преобразова­ние	У (0	Y(P)
Сложение оригинала	У (0 4 У* (0	Yi (Р) 4- Ка (р)
Умножение на постоян­ное число	ау (0	оУ (р)
Дифференцирование	dy/di dyldt, Уо = 0	PY (р) — Уо рК(р)
п-кратнос дифференци-	dnyldtn	pnY (р) — [рп_1р°4-
рование	dnyldtn при нулевых начальных условиях t	4-р" 2{/о4- • • • 4- Уо *1 PnY (р)
Интегрирование	j У (f)dt	-уУ(р)
Сдвиг оригинала на г	У(1-т)	t~pxY (р)

вблизи t = 0, т. е. в самом начале двияЛиия, и вблизи t = оо, т. е. для боль-‘ ших t, при условии, что система устойчива*

Эту задачу можно решить с помощью следующих теорем о предельном переходе (предельных свойств преобразований Лапласа):

1. Если существует предел функции Нш [у то

Нш [у «)],->„ = Нш pY (р)]р^те. (15.25)

2. Если существует предел функции Нш [у (<)]*_►<»> то

Нт [у (Ol^oo — Нш [pY (р)]^0. (15.26)

Из этих формул видно, что для определения предельных значений функции у (0 надо подставить в ее изображение, умноженное на р, значение р = оо или Р = 0.

В качестве примера рассмотрим решение дифференциального уравнения второго порядка операторным методом [11]

8+аіУ+аоУ = х (<)• (15.27)

Переходя от оригиналов у (<) и х (1) к изображениям по формулам, приведенным в табл. 15.1, получим изображение уравнения (15.27) в виде

аіУо 4~ Уо____ і ___________ Р_______ Ра 4~ аі Р + Оо 0 Р* + OlP + оо

Р* Ч" Охр + Оо J +’ VtL~l [

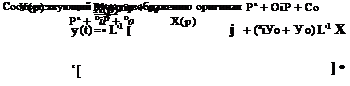(р®’+ ахр + со) Y (р) = X (р) + 6о + (fli + Р) Уо — Отсюда найдем изображение Y (р) функции у (1)

Г 1 1	eptt__ ep*t	1-і Г P ]
L Р2 + <hP + ао J	Pi — Pi	— [ p2 + alP — f — a0 J

Предполагается, что корни рг и р2 знаменателя ра + агр + а0 простые и дей­ствительные. По таблицам перехода от изображений к оригиналам находим

РіЄ‘

Pit.

■р2е

Pit

Х(Р)

У (О ^ • 1 •….. 1 ІРо + (с, + Pi) Pol ер,< — [Ро + (С! + р2) р0еР2< )• (15.29)

Pi — Ра

Аналогично можно получить решение и для случая комплексных или кратных корней уравнения р2 + агр + (ц — 0.

Подобным образом можно осуществить решение’дифференциальных уравнений более высоких порядков или систем уравнений.

Достоинство операторного метода состоит в том, что объем и сложность вычисли­тельных работ получается меньшим по сравнению с классическим методом. При операторном методе отпадает трудоемкая операция определения произвольных постоянных из условия удовлетворения заданным начальным условиям, так как сразу находится решение дифференциальных уравнений, удовлетворяющее этим условиям.